Introduction
Imagine a student learning algebra: if they practice only one method to solve an equation, their understanding remains fragile. But when they explore multiple approaches through trial, error, and feedback, their skills deepen. This principle isn’t just true for humans. A new method called Reinforced Fine-Tuning (ReFT) uses a similar strategy for large language models (LLMs) — allowing them to solve complex math problems more easily.
Limitations
Today’s AI models often learn through supervised fine-tuning (SFT), which is like memorizing step-by-step solutions from a textbook.
In math, for example models follow predefined reasoning paths known as “chains of thought” (CoTs) - but most datasets provide only one correct method per problem. This makes it hard for them to adapt to new problems. For example, SFT-trained models don’t improve their performance when faced with new problems.
As one researcher explains: “They learn the steps but don’t truly understand why they work.”
A New Approach: Learning through Trial and Error
Moving away from the limitations of traditional SFT and exploring new approaches: learning through trial and error. This raises the question: Can LLMs reason better with reinforcement learning?
Introducing Reinforced Fine-Tuning (ReFT), a method that combines initial supervised training with reinforcement learning (RL). This allows models to generate multiple solutions and learn from their outcomes.
OpenAI Approach
During the “12 days of OpenAI” event, OpenAI introduced a new fine-tuning technique — Reinforcement fine-tuning (ReFT) — that rethinks how models are trained.
Instead of the typical fine-tuning process, where the model simply tries to reproduce the labeled target answer, ReFT trains the model to develop its own reasoning process that leads to correct answers.
The approach introduces customizable “graders” that score the model’s outputs, turning each evaluation into a reward signal.
This reward signal helps the model through multiple rounds of training, gradually enhancing its performance based on feedback.
How ReFT Diverges from Supervised Fine-Tuning (SFT)
Table 1: Comparison between SFT and OpenAI ReFT
| Aspect | SFT | OpenAI ReFT |
|---|---|---|
| Dataset Preparation | Structured, labeled dataset (split into training and validation sets) provides the model with foundational knowledge | Same foundational approach |
| Evaluation Method | Model imitates labeled targets | Model develops reasoning, guided by “Graders” that score outputs (e.g., 0 to 1) |
| Training Approach | Direct imitation learning | Reward-based tuning - model’s output is scored, weights adjusted to maximize future rewards |
| Improvement Strategy | Static learning from examples | Iterative improvement - repeated fine-tuning cycles refine the model’s strategy |
This process helps the model learn meaningful strategies rather than just replicating answers.
We won’t know if this approach works until we finish the evaluation phase. The results of ReFT shown below compares a fine-tuned o1-mini with a standard o1-mini and o1 model and with just 1,100 samples of data, and it’s even more accurate than the o1, even though the latter is larger and more advanced.
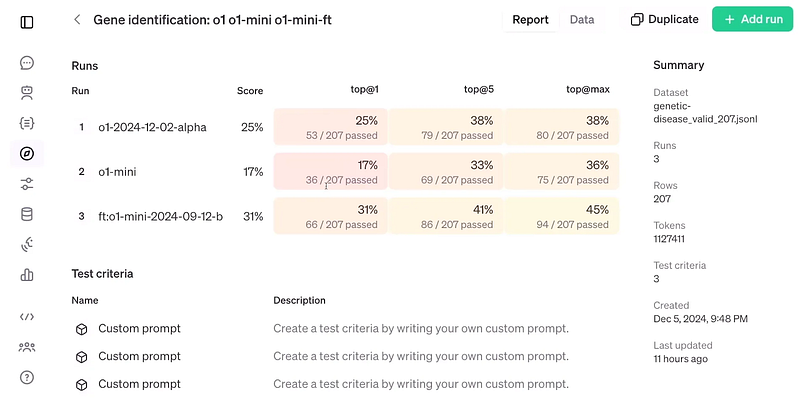 Figure 1: Evaluation of OpenAI ReFT (source: OpenAI)
Figure 1: Evaluation of OpenAI ReFT (source: OpenAI)
ByteDance Approach (ReFT: Reinforced Fine-tuning)
Switching from OpenAI’s grader-guided fine-tuning to ByteDance’s dynamic Reinforced Fine-Tuning, which explores multiple ways of thinking to create better reasoning strategies.
While OpenAI’s ReFT focuses on general tasks, ByteDance focuses on math problem solving. The authors mentioned that one way to enhance the reasoning capability of Large Language Models (LLMs) is to conduct Supervised Fine-Tuning (SFT) using Chain-of-Thought (CoT) annotations.
However, because this approach relies only on the given CoT data, it doesn’t generalize well. In addition, in math problem-solving there is only one annotated path for each question which can be much better for the algorithm to learn from multiple annotated paths given one single question. So to address limitations in existing math problem-solving methods, ByteDance research team proposed new technique which is ReFT.
ByteDance’s ReFT takes a different approach. Instead of relying on static examples, it combines initial supervised training with reinforcement learning (RL) - a trial-and-error process where the model generates multiple solutions and learns from their outcomes.
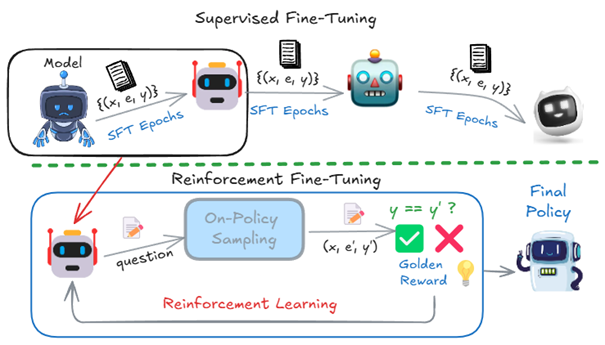 Figure 2: An example of question (x), CoT (e), and answer (y) in GSM8K
Figure 2: An example of question (x), CoT (e), and answer (y) in GSM8K
How ReFT Works
ReFT can be split into two main phases which we will see in details.
1. Warm-Up Phase with SFT
In this phase the model first learns the basic problem-solving skills with SFT, much like a student reviewing foundational concepts. In other words, this establishes a baseline reasoning ability.
The policy therefore is fine-tuned for a few epochs on a dataset comprising of the “(question, CoT)” tuples: (x,e) as shown in Figure 2. This would enable it to have basic problem-solving skills using a dataset comprising of (question, answer) tuples: (x,y).
2. Online Reinforcement Learning (PPO)
Exploration phase with PPO (Proximal Policy Optimization): The model enters an exploration phase where it uses PPO to generate multiple reasoning paths.
Reward mechanism:
- If answer is correct: get full points (1)
- If answer is wrong: no points (0)
- If the answer is a number: a partial reward (0.1) might be given if response is partly correct
Stabilizing training with PPO: This algorithm stabilizes the training by limiting policy updates to prevent larger deviations from the initial policy, ensuring stable and gradual improvements.
All attempts are created “on-policy,” meaning they come from the model’s current understanding.
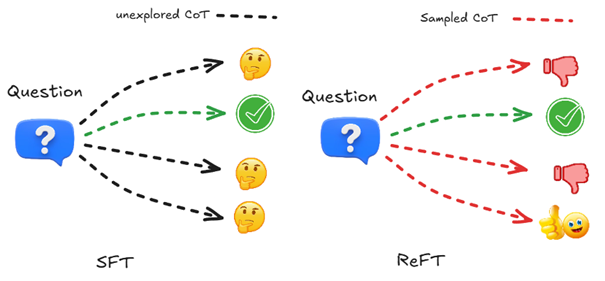 Figure 3: Comparison between SFT and ReFT on the presence of CoT alternatives
Figure 3: Comparison between SFT and ReFT on the presence of CoT alternatives
Datasets and Models
The experiments were conducted on three datasets: GSM8K, SVAMP, and MathQA.
- GSM8K and SVAMP show answers as numbers
- MathQA shows answers as a list of possible answers
- Both N-CoT (natural language) and P-CoT (program-based chain-of-thought) annotations were generated using few-shot prompting with GPT-3.5
The study focused on two foundational models: Galactica-6.7B and CodeLLAMA-7B - these two known for their strong performance in math problem-solving and are widely adopted in reasoning tasks.
Evaluation was based on 100 examples of chain-of-thought, using value accuracy metrics for both N-CoT and P-CoT for all datasets.
Beyond baseline comparisons, common techniques such as majority voting and reward model reranking were applied to GSM8K. The training process utilized high-performance hardware with carefully tuned settings for warm-up duration and learning rate.
Results
ReFT outperforms SFT most of the time, except for MathQAMCQ N-CoT. Specifically, this technique has improved by 10 and 12 points compared to SFT with CodeLLAMA on GSM8K N-CoT and P-CoT, respectively.
Also on average, it improves by 6.7 and 7.4 points with CodeLLAMA on all sets in N-CoT and P-CoT, respectively as you can see in Table 2.
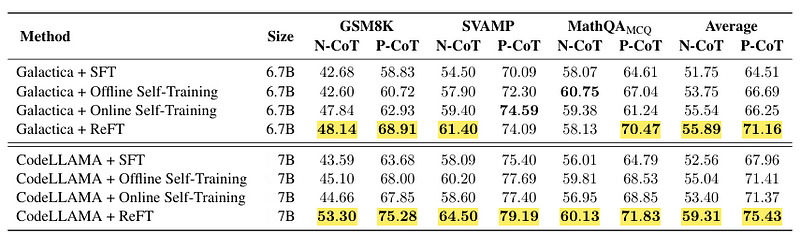 Table 2: Value accuracy of ReFT and the baselines fine-tuned with two foundation models on all datasets
Table 2: Value accuracy of ReFT and the baselines fine-tuned with two foundation models on all datasets
Challenges and Road Ahead
As you may know, no technique is flawless, so despite its promise, ReFT faces some challenges:
Training Efficiency
ReFT needs a greater number of epochs to reach convergence compared to SFT due to the fact that ReFT requires exploration of the generation space to find correct answers.
To speed up reaching the convergence:
- Higher learning rate might help, but it could also make the policy more unstable and could possibly collapse
- Larger batch size is another option, however it comes at the expense of increased computational costs
Reward Hacking
Experiments on MathQAMCQ N-CoT dataset showed that the policy can be manipulated if the possible space of the final answer is limited like MCQs (Multiple Choice Questions) like in the example shown in Figure 4.
 Figure 4: Example prediction of MathQAMCQ reveals reward hacking
Figure 4: Example prediction of MathQAMCQ reveals reward hacking
To deal with the reward hacking issue, it would be possible to try a detailed or process-based reward function that takes into account a broader range of factors.
Future Work
Future work could include:
- Using offline reinforcement learning techniques
- Developing a warm-up free method to improve training efficiency and performance
- Applying a well-trained process-based reward model (PRM) can enhance its performance as researchers suggested
- It could be applied to more general reasoning tasks
Majority Voting and Reranking Benefit ReFT
On top of that, ReFT leverages majority voting and reward model reranking, surpassing SFT in performance, as shown in Table 3. Among open-source methods, its best variant excels, particularly in the CodeLLAMA + ReFT + Reranking setup, achieving impressive accuracy and even competing with GPT-3.5-turbo despite being a smaller 7B model.
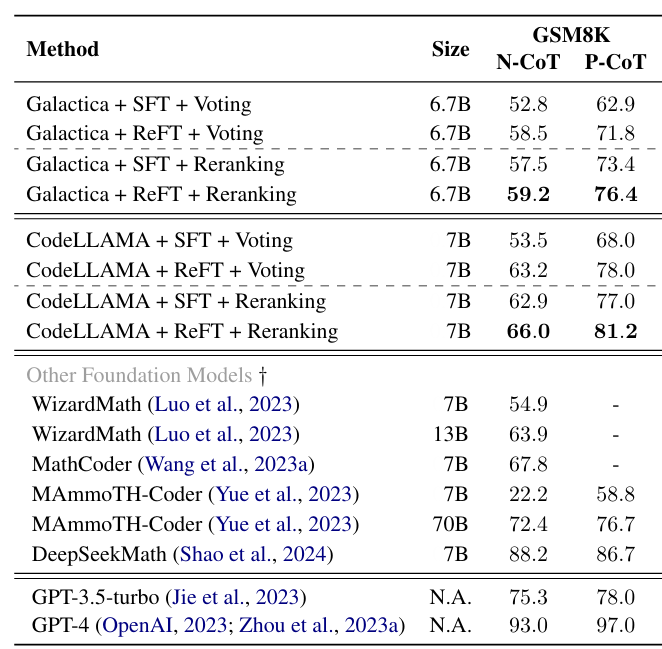 Table 3: Solving accuracy of majority voting and reward model reranking for SFT and ReFT on GSM8K
Table 3: Solving accuracy of majority voting and reward model reranking for SFT and ReFT on GSM8K
Conclusion
Reinforcement fine-tuning (ReFT) is a sophisticated approach that offers the ability to adapt LLMs for specific use cases. This approach applies RL specifically using PPO algorithm to fine-tune LLMs for math problem solving.
As the researchers conclude: “The goal isn’t just accuracy - it’s understanding.” And in that pursuit, ReFT offers a promising blueprint for building systems that not only compute, but reason.
References
- Proximal Policy Optimization Algorithms (PPO)
- Design of Chain-of-Thought in Math Problem Solving
- Chain-of-Thought Prompting Elicits Reasoning in Large Language Models
(END)